Čo sú dvojky v sudoku? O metódach riešenia problémov - kompletný kurz sudoku

SUDOKU je populárna hra- hlavolam, čo je hlavolam s číslami, ktorý sa dá prekonať iba budovaním logických záverov. V mene sudoku v preklade z japončiny „su“ znamená „číslo“ a doku „doku“ znamená „stáť sám“. Preto „SUDOKU“ v hrubom preklade znamená „jednociferné“.

Názov „Sudoku“ dalo tejto skladačke japonské vydavateľstvo Nicoli v roku 1984. Sudoku je skratka pre „Suuji wa dokushin ni kagiru“, čo v japončine znamená „číslo musí byť jednotné“. Vydavateľstvo Nikoli neprišlo len so zvučným názvom, ale po prvý raz zaviedlo aj symetriu v úlohách pre svoje hlavolamy. Názov hlavolamu dala hlava Nicoli - Kaji Maki. Tento nový japonský názov prijal celý svet, no v samotnom Japonsku sa hlavolam volá „Nanpure“. Nicoli si vo svojej krajine zaregistrovala slovo „Sudoku“ ako ochrannú známku.

História vzniku SUDOKU

India je považovaná za rodisko šachu a Anglicko je považované za rodisko futbalu. Hra Sudoku, ktorá sa rýchlo rozšírila do celého sveta, nemá ako takú domovinu. Za prototyp sudoku možno považovať hlavolam „Magic Square“, ktorý sa objavil v Číne pred 2000 rokmi.

História Sudoku ako hry siaha až k menu slávneho švajčiarskeho matematika, mechanika a fyzika Leonharda Eulera (1707 - 1783).

Dokumenty v jeho archívoch zo 17. októbra 1776 obsahujú poznámky o tom, ako vytvoriť magický štvorec s určitým počtom buniek, najmä 9, 16, 25 a 36. V ďalšom dokumente s názvom „Vedecké skúmanie nových odrôd magického štvorca “, Euler umiestnený v bunkách sú latinské písmená (latinský štvorec), neskôr vyplnil bunky gréckymi písmenami a štvorec nazval grécko-latinským. Pri skúmaní rôznych verzií magického štvorca Euler upozornil na problém kombinovania symbolov tak, aby sa ani jeden neopakoval v žiadnom riadku či stĺpci.

Sudoku v ich modernej podobe boli prvýkrát publikované v roku 1979 v časopise Word Games. Autorom skladačky bol Harvard Garys z Indiany. Hádanka „Number Place“ (preložená do ruštiny ako „miesto čísla“) - to možno považovať za jedno z prvých vydaní moderného sudoku. Pridal 3 x 3 štvorcové bloky, čo bolo dôležité zlepšenie, pretože to urobilo hádanku zaujímavejšou. Použil Eulerov princíp latinského štvorca, aplikoval ho na maticu 9x9 a pridal ďalšie obmedzenia, čísla by sa vo vnútorných štvorcoch 3x3 nemali opakovať.

Myšlienka sudoku teda nepochádza z Japonska, ako si mnohí myslia, ale názov hry je skutočne japonský.

V Japonsku bol tento hlavolam publikovaný Nicoly Inc., významným vydavateľom zbierok rôznych hlavolamov, v novinách Monthly Nicolist v apríli 1984 pod názvom "Číslo možno použiť iba raz." 12. novembra 2004 noviny The Times po prvýkrát zverejnili na svojich stránkach hlavolam Sudoku. Táto publikácia sa stala senzáciou, hádanka sa rýchlo rozšírila po celej Británii, Austrálii a na Novom Zélande; získal popularitu v USA.

Variácie sudoku

Čo je teda sudoku? V súčasnosti existuje veľa modernizácií pre tento populárny typ hádaniek, ale klasické sudoku je štvorec 9x9, rozdelený na podštvorce so stranami po 3 bunky. Celkové hracie pole je teda 81 buniek. V prílohe mojej práce uvediem odlišné typy Sudoku a riešenia (pomohli mi ich vyriešiť rodičia).

Sudoku sa líši v úrovni obtiažnosti v závislosti od veľkosti štvorca:

• 1. Pre malých milovníkov hádaniek urobte sudoku s políčkami 2x2, 6x6 buniek.
• 2. Pre profesionálov sú tu sudoku 15x15 a 16x16 buniek

Sudoku prichádza v rôznych úrovniach:

• ľahké
• priemer
• ťažké
• veľmi komplikované
• super komplex

Pravidlá riešenia

Sudoku majú len jedno pravidlo. Je potrebné vyplniť prázdne bunky tak, aby sa v každom riadku, v každom stĺpci a v každom malom štvorci 3X3 každé číslo od 1 do 9 objavilo iba raz. Niektoré bunky v Sudoku sú už zaplnené číslami a zvyšok už stačí vyplniť. Ako viac čísel náklady na začiatku, tým ľahšie je vyriešiť hádanku. Mimochodom, správne zostavené sudoku má len jedno riešenie.

Riešenie sudoku

Stratégia riešenia sudoku zahŕňa tri fázy:

• naučiť sa umiestňovať čísla v hádanke
• predbežné usporiadanie čísel
• analýza

Najlepšia cesta riešenia - čísla kandidátov napíšte do ľavého horného rohu bunky. Potom môžete presne vidieť čísla, ktoré by mali zaberať túto bunku. Sudoku by sa malo hrať pomaly, pretože je to relaxačná hra. Niektoré hádanky sa dajú vyriešiť za pár minút, iné však môžu trvať hodiny alebo v niektorých prípadoch aj dni.

Matematický základ. Počet možných kombinácií v sudoku 9x9 je podľa výpočtov Berthama Felgenhauera 6 670 903 752 021 072 936 960.

Čo vám pomôže rozvinúť jeden z najdôležitejšie orgány- mozog. Samozrejme, medzi ne patria aj známe japonské hlavolamy Sudoku. S ich pomocou môžete výrazne „napumpovať svoj mozog“, pretože okrem potreby vypočítať obrovské množstvo možností usporiadania čísel musíte byť schopní to urobiť aj niekoľko desiatok ťahov dopredu. Jedným slovom, toto je skutočný raj, ak chcete zabrániť vysychaniu vašich neurónov. A dnes sa pozrieme na základné techniky, ktoré používajú experti na sudoku. To bude užitočné pre začiatočníkov aj pre dlhoročných fanúšikov týchto hádaniek. Koniec koncov, niekto potrebuje urobiť prvé kroky v umení sudoku a niekto potrebuje zlepšiť efektivitu svojich rozhodnutí!

pravidlá

Ak ešte nie ste oboznámení, mali by ste sa najskôr oboznámiť s pravidlami. Verte mi, sú veľmi jednoduché.

Hracie pole je štvorec s rozmermi 9x9. Zároveň je rozdelená na menšie štvorce s rozmermi 3x3. To znamená, že celé pole pozostáva z 81 buniek.

Podmienkou problému sú čísla, ktoré sú už v týchto bunkách umiestnené.

Blok (blok buniek) je malý štvorec, riadok alebo čiara.

Čo je potrebné urobiť: usporiadať všetky zostávajúce čísla podľa niekoľkých pravidiel. Po prvé, v každom z malých štvorcov by nemali byť žiadne opakovania. Po druhé, vo všetkých stĺpcoch a riadkoch by sa nemali opakovať. To znamená, že každé číslo by sa malo v každom z týchto blokov objaviť iba raz. Aby bolo všetko ešte jasnejšie, venujte pozornosť vyriešenému sudoku:

Základné riešenie

Spravidla, ak riešite jednoduché sudoku, stačí si do každej z 81 políčok zapísať všetky možné možnosti a postupne odškrtávať nevhodné možnosti. Je to veľmi jednoduché.

Ak sa však posuniete o úroveň vyššie k zložitejšiemu sudoku, veci budú zaujímavejšie. Často sa stane, že neexistuje spôsob, ako dať nové čísla, a budete musieť prejsť predpokladmi: „Nech je tu také číslo“, potom budete musieť zvážiť túto hypotézu a buď prísť k riešeniu. na problém alebo na rozpor s vaším predpokladom.

Ale samozrejme, existujú špeciálne techniky, ktoré vám to všetko pomôžu robiť efektívnejšie.

Techniky

1. Nahé dvojice/trojky/štvorky

Ak máte dve bunky v jednom bloku (štvorec, riadok alebo stĺpec), do ktorých môžete vložiť iba 2 čísla, potom tieto čísla môžu byť samozrejme odstránené z možných možností pre ostatné bunky v tomto bloku.

Okrem toho sa tento trik dá ľahko vykonať s trojicou aj štvoricou:

2. Skryté páry

Veľmi užitočný trik, v niektorých ohľadoch opak nahých párov. Ak v niektorých dvoch bunkách jedného štvorca v „možných možnostiach“ máte čísla, ktoré sa nikde inde (v tomto štvorci) neopakujú, potom všetky ostatné čísla z týchto dvoch buniek môžu byť odstránené.

Aby to bolo ešte jasnejšie, venujte pozornosť príkladom (jeden jednoduchý a jeden zložitejší):

Našťastie to funguje pre trojky aj štvorky, ale stojí za zmienku veľmi dôležitá a veľmi skvelá funkcia. Nie je potrebné, aby tri/štyri bunky obsahovali rovnaké 3 číslice tvaru (a;b;c) (a;b;c) (a;b;c). Táto možnosť vám bude stačiť: (a;b) (b;c) (a;c).

3. Nepomenované pravidlo

Ak máte v jednom stĺpci/riadku dvojicu alebo trojicu, ktoré sa nachádzajú v rovnakom štvorci, môžete tieto čísla pokojne odstrániť z iných buniek tohto štvorca.

4. Ukazovacie dvojice

Ak sú v jednom riadku/stĺpci v „možných možnostiach“ dve rovnaké čísla, potom je možné takéto čísla z príslušného stĺpca/riadku odstrániť.

To môže byť niekedy veľmi užitočné, najmä ak nájdete niekoľko z týchto párov:

Samozrejme, v tomto prípade musia tieto čísla chýbať v iných bunkách štvorca, ale podľa bezmenného pravidla sa to nevyžaduje.

Milujte sudoku a ďalšie vývojové hádanky, hry, hádanky a testy rôzne aspekty myslenie? Získajte prístup ku všetkým interaktívnym materiálom na stránke, aby ste sa mohli vyvíjať efektívnejšie.

Záver

Pozreli sme sa na základné techniky, ktoré sa používajú pri riešení sudoku. Podotýkam, že toto je len začiatok a v nasledujúcich článkoch sa pozrieme na zložitejšie a zaujímavejšie funkcie, vďaka ktorým bude riešenie takýchto problémov ešte zaujímavejšie a jednoduchšie.

Ako tréning vás redakcia 4brain pozýva, aby ste sa zoznámili so súborom, ktorý obsahuje sudoku rôznych úrovní obtiažnosti. Nájdite si čas na cvičenie, pretože ak tejto činnosti venujete dostatok času, tak sa na konci tohto chodu článkov, verte, stanete skutočným esom v riešení japonských hlavolamov.

Ak máte nejaké otázky o týchto technikách alebo o Sudoku, ktoré prikladáme k článku, pokojne sa ich spýtajte v komentároch!

Prvá vec, ktorá by mala byť stanovená v metodológii riešenia problémov, je otázka skutočného pochopenia toho, čo dosahujeme a môžeme dosiahnuť v otázkach riešenia problémov. Pochopenie sa zvyčajne považuje za samozrejmosť a strácame zo zreteľa, že porozumenie má určitý východiskový bod porozumenia, iba vo vzťahu ku ktorému môžeme povedať, že porozumenie skutočne prebieha od konkrétneho okamihu, ktorý sme si určili. Sudoku je tu podľa nášho názoru vhodné v tom, že nám umožňuje do určitej miery modelovať otázky porozumenia a riešenia problémov. Začneme však trochu inými a nemenej dôležitými príkladmi ako sudoku.

Fyzik študujúci špeciálnu teóriu relativity môže hovoriť o Einsteinových „krištáľovo čistých“ propozíciách. Na túto frázu som narazil na jednej zo stránok na internete. Ale kde začína toto chápanie „kryštálovej čistoty“? Začína to porozumením matematický zápis postulátov, z ktorých možno postaviť všetky viacposchodové matematické štruktúry SRT podľa známych a zrozumiteľných pravidiel. Čomu však fyzik, rovnako ako ja, nerozumie je, prečo postuláty SRT fungujú práve týmto spôsobom a nie inak.

Po prvé, drvivá väčšina diskutujúcich o tejto doktríne nerozumie tomu, čo presne je v postuláte nemennosti rýchlosti svetla, keď sa prenesie z jeho matematickej aplikácie na realitu. A tento postulát implikuje stálosť rýchlosti svetla vo všetkých mysliteľných a nepredstaviteľných zmysloch. Rýchlosť svetla je konštantná vo vzťahu k akýmkoľvek objektom, ktoré sú v pokoji a pohybujú sa súčasne. Rýchlosť svetelného lúča je podľa postulátu konštantná aj vzhľadom na prichádzajúci, priečny a ustupujúci svetelný lúč. A zároveň v skutočnosti máme len merania nepriamo súvisiace s rýchlosťou svetla, interpretovanou ako jeho stálosť.

Newtonove zákony sú tak známe fyzikom a dokonca aj tým, ktorí jednoducho študujú fyziku, že sa zdajú také pochopiteľné, ako niečo samozrejmé a nemôže to byť inak. Ale povedzme aplikácia zákona univerzálna gravitácia začína jeho matematickým zápisom, z ktorého sa dajú vypočítať dokonca aj trajektórie vesmírnych objektov a orbitálne charakteristiky. Ale nerozumieme tomu, prečo tieto zákony fungujú tak a nie inak.

To isté so Sudoku. Na internete môžete nájsť opakované popisy „základných“ spôsobov riešenia problémov sudoku. Ak si pamätáte tieto pravidlá, môžete pochopiť, ako sa tento alebo ten problém sudoku rieši použitím „základných“ pravidiel. Ale mám otázku: chápeme, prečo tieto „základné“ metódy fungujú tak, ako fungujú, a nie inak.

Prejdeme teda k ďalšiemu kľúčovému bodu v metodológii riešenia problémov. Pochopenie je možné len na základe nejakého modelu, ktorý poskytuje základ pre toto porozumenie a možnosť uskutočniť nejaký prirodzený alebo mentálny experiment. Bez toho môžeme mať iba pravidlá na uplatňovanie zapamätaných východiskových bodov: postuláty SRT, Newtonove zákony alebo „základné“ metódy v Sudoku.

Nemáme a v zásade ani nemôžeme mať modely, ktoré spĺňajú postulát neobmedzenej stálosti rýchlosti svetla. Nemáme, ale dajú sa vymyslieť nepreukázateľné modely, ktoré sú v súlade s Newtonovými zákonmi. A existujú také „newtonovské“ modely, ale nejako nezapôsobia svojimi produktívnymi schopnosťami na vykonávanie rozsiahleho alebo myšlienkového experimentu. Sudoku nám však poskytuje príležitosti, ktoré môžeme využiť na pochopenie samotných problémov sudoku a na ilustráciu modelovania ako všeobecného prístupu k riešeniu problémov.

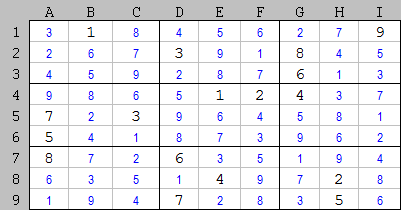
Jedným z možných modelov problémov so sudoku je pracovný list. Vytvorí sa jednoduchým vyplnením všetkých prázdnych buniek (buniek) tabuľky špecifikovanej v úlohe číslami 123456789. Ďalej je úlohou postupne odstraňovať všetky nadbytočné číslice z buniek, kým sa všetky bunky tabuľky nezaplnia jediné (výlučné) číslice, ktoré spĺňajú podmienky úlohy.

Vytvorím takýto pracovný list v Exceli. Najprv vyberiem všetky prázdne bunky (bunky) tabuľky. Stlačím F5 - "Vybrať" - "Prázdne bunky" - "OK". Všeobecnejší spôsob výberu požadovaných buniek: podržte Ctrl a kliknite myšou na výber týchto buniek. Potom pre vybrané bunky nastavím Modrá farba, veľkosť 10 (pôvodná 12) a písmo Arial Narrow. To všetko preto, aby boli následné zmeny v tabuľke jasne viditeľné. Ďalej do prázdnych buniek zadávam čísla 123456789 nasledujúcim spôsobom: Toto číslo si zapíšem a uložím do samostatnej bunky. Potom stlačím F2, vyberiem a skopírujem toto číslo pomocou Ctrl+C. Ďalej prejdem k bunkám tabuľky a postupne prechádzam cez všetky prázdne bunky a pomocou operácie Ctrl + V do nich zadávam číslo 123456789 a pracovný hárok je pripravený.

Extra čísla, o ktorých sa bude diskutovať neskôr, odstraňujem nasledovne. Pomocou operácie Ctrl+kliknutie vyberiem bunky s číslom navyše. Potom stlačím Ctrl+H a do horného poľa okna, ktoré sa otvorí, zadá číslo, ktoré sa má vymazať, pričom spodné pole by malo byť úplne prázdne. Ďalej stačí kliknúť na možnosť „Nahradiť všetko“ a ďalšia číslica sa odstráni.

Súdiac podľa toho, že zvyčajne viem robiť pokročilejšie spracovanie tabuliek bežnými „základnými“ spôsobmi ako v príkladoch uvedených na internete, pracovný list je najjednoduchší nástroj na riešenie úloh sudoku. Navyše veľa situácií týkajúcich sa aplikácie najkomplexnejších z takzvaných „základných“ pravidiel v mojom pracovnom liste jednoducho nenastalo.

Pracovný list je zároveň aj modelom, na ktorom môžete robiť experimenty s následnou identifikáciou všetkých „základných“ pravidiel a rôznych nuancií ich aplikácie vyplývajúcich z experimentov.

Takže tu je fragment pracovného hárka s deviatimi blokmi očíslovanými zľava doprava a zhora nadol. V tomto prípade máme štvrtý blok vyplnený číslami 123456789. Toto je náš model. Mimo bloku sme červenou farbou zvýraznili „aktivované“ (konečne určené) čísla, v tomto prípade štvorky, ktoré mienime vložiť do zostavovanej tabuľky. Modré päťky sú čísla, ktoré ešte nie sú určené, pokiaľ ide o ich budúcu úlohu, o ktorej si povieme neskôr. Aktivované čísla, ktoré sme priradili, sú akoby prečiarknuté, vytlačené, vymazané - vo všeobecnosti premiestňujú čísla rovnakého mena v bloku, takže sú tam znázornené bledou farbou, čo symbolizuje skutočnosť, že tieto bledé čísla sú vymazané. Chcel som urobiť túto farbu ešte bledšou, ale potom by sa mohli stať úplne neviditeľnými pri prezeraní na internete.

Výsledkom bolo, že vo štvrtom bloku v bunke E5 bol jeden, tiež aktivovaný, ale skrytý štyri. „Aktivovaný“, pretože môže tiež odstrániť nepotrebné číslice, ak sa nejaké objavia v jeho ceste, a „skrytý“, pretože sa nachádza medzi ostatnými číslicami. Ak je bunka E5 napadnutá zvyšnými, okrem 4, aktivovanými číslami 12356789, potom sa v E5 - 4 objaví „nahý“ singleton.

Teraz odstránime jednu aktivovanú štvorku, napríklad z F7. Potom štvorka vo vyplnenom bloku môže skončiť užšia a iba v bunke E5 alebo F5, pričom zostane aktivovaná v riadku 5. Ak sa aktivované päťky dostanú do tejto situácie, bez F7=4 a F8=5, potom sa aktivuje holá alebo skrytá pár 45.

Potom, čo ste dostatočne pracovali a pochopili rôzne možnosti s nahými a skrytými singlami, dvojkami, trojkami atď. nielen v blokoch, ale aj v riadkoch a stĺpcoch, môžeme prejsť na ďalší experiment. Vytvorme holú dvojicu 45, ako to bolo urobené predtým, a potom spojíme aktivované F7=4 a F8=5. V dôsledku toho vznikne situácia E5=45. K takýmto situáciám veľmi často dochádza pri spracovaní pracovného listu. Táto situácia znamená, že jedna z týchto číslic, v tomto prípade 4 alebo 5, musí byť v bloku, riadku a stĺpci, ktorý obsahuje bunku E5, pretože vo všetkých týchto prípadoch musia byť dve číslice, nie iba jedna z nich.

A čo je najdôležitejšie, teraz už vieme, ako často vznikajú situácie ako E5=45. Rovnakým spôsobom zadefinujeme situácie, keď sa v jednej bunke objavia tri číslice atď. A keď privedieme mieru pochopenia a vnímania týchto situácií do stavu samozrejmosti a jednoduchosti, potom ďalším krokom je, takpovediac, vedecké pochopenie situácií: potom budeme môcť urobiť štatistickú analýzu sudoku, identifikujte vzory a použite nahromadený materiál na riešenie najzložitejších problémov.

Experimentovaním na modeli teda získame vizuálnu a dokonca „vedeckú“ reprezentáciu skrytých alebo otvorených singlov, párov, trojíc atď. Ak sa obmedzíte iba na prácu s opísaným jednoduchým modelom, niektoré vaše nápady sa ukážu ako nepresné alebo dokonca chybné. Len čo však prejdete k riešeniu konkrétnych problémov, rýchlo sa ukážu nepresnosti prvotných myšlienok a modely, na ktorých sa experimenty robili, bude treba premyslieť a dolaďovať. Toto je nevyhnutná cesta hypotéz a objasnení pri riešení akýchkoľvek problémov.

Treba povedať, že skryté a otvorené singly, ako aj otvorené dvojice, trojičky a dokonca štvorky sú bežné situácie, ktoré vznikajú pri riešení úloh sudoku s pracovným listom. Skryté páry boli zriedkavé. Ale tu sú skryté trojky, štvorky atď. Pri spracovaní pracovných listov som sa akosi nestretol s metódami „x-wing“ a „swordfish“ na obchádzanie kontúr, ktoré boli opakovane opísané na internete, v ktorých „kandidáti“ na vymazanie vznikajú v ktorejkoľvek z dvoch alternatív. metódy obchádzania obrysov. Význam týchto metód: ak zničíme „kandidáta“ x1, zostane výhradný kandidát x2 a zároveň sa vymaže kandidát x3, a ak zničíme x2, zostane výhradný kandidát x1, ale v tomto prípade kandidát x3 je tiež vymazané, takže x3 by malo byť v každom prípade vymazané, zatiaľ bez ovplyvnenia kandidátov x1 a x2. Všeobecnejšie povedané, toto špeciálny prípad situácie: ak dve alternatívne metódy vedú k rovnakému výsledku, potom tento výsledok možno použiť na vyriešenie problému sudoku. Stretol som sa so situáciami v tomto všeobecnejšom zmysle, nie však vo variantoch „x-wing“ a „swordfish“ a nie pri riešení úloh Sudoku, na ktoré postačia znalosti len „základných“ prístupov.

Vlastnosti používania pracovného hárka možno ukázať na nasledujúcom netriviálnom príklade. Na jednom z fór riešiteľov sudoku http://zforum.net/index.php?topic=3955.25;wap2 som narazil na problém prezentovaný ako jeden z najťažších problémov sudoku, ktorý nemožno vyriešiť konvenčnými metódami bez použitia hrubá sila s predpokladmi týkajúcimi sa čísiel vložených do buniek . Ukážeme, že s pracovným listom môžete vyriešiť tento problém bez takého vyčerpávajúceho hľadania:

Vpravo je pôvodná úloha, vľavo je pracovný list po „preškrtnutí“, t.j. rutinná operácia odstraňovania nadbytočných číslic.

Najprv sa dohodneme na notácii. ABC4=689 znamená, že bunky A4, B4 a C4 obsahujú čísla 6, 8 a 9 – jedna alebo viac číslic na bunku. Rovnako je to aj so šnúrkami. Takže B56=24 znamená, že bunky B5 a B6 obsahujú čísla 2 a 4. Znak ">" je znakom podmienenej akcie. D4=5>I4-37 teda znamená, že v dôsledku správy D4=5 by sa číslo 37 malo umiestniť do bunky I4. Správa môže byť explicitná – „nahá“ – a skrytá, čo musí byť odhalené. Vplyv správy môže byť sekvenčný (prenesený nepriamo) pozdĺž reťazca alebo paralelný (vplyv priamo na iné bunky). Napríklad:

D3=2; D8=1>A9-1>A2-2>A3-4,G9-3; (D8=1)+(G9=3)>G8-7>G7-1>G5-5

Tento záznam znamená, že D3=2, ale túto skutočnosť je potrebné odhaliť. D8=1 prenáša svoj vplyv na A3 pozdĺž reťazca a 4 by sa malo zapísať do A3; súčasne D3=2 pôsobí priamo na G9, výsledkom čoho je výsledok G9-3. (D8=1)+(G9=3)>G8-7 – kombinovaný vplyv faktorov (D8=1) a (G9=3) vedie k výsledku G8-7. A tak ďalej.

Záznamy môžu obsahovať aj kombinácie ako H56/68. To znamená, že čísla 6 a 8 sú v bunkách H5 a H6 zakázané, t.j. mali by byť z týchto buniek odstránené.

Začnime teda pracovať s tabuľkou a najprv aplikujme dobre vyvinutú, nápadnú podmienku ABC4=689. To znamená, že vo všetkých ostatných bunkách (okrem A4, B4 a C4) bloku 4 (v strede, vľavo) a 4. riadku musia byť odstránené čísla 6, 8 a 9:

Rovnakým spôsobom použijeme B56=24. Celkovo máme D4=5 a (po D4=5>I4-37) HI4=37 a tiež (po B56=24>C6-1) C6=1. Aplikujme to na pracovný list:

V I89=68skryté>I56/68>H56-68: t.j. v bunkách I8 a I9 je skrytá dvojica číslic 5 a 6, ktorá zakazuje prítomnosť týchto číslic v I56, čo vedie k výsledku H56-68. Tento fragment môžeme posudzovať inak, rovnako ako sme to urobili v experimentoch na modeli pracovného hárka: (G23=68)+(AD7=68)>I89-68; (I89=68)+(ABC4=689)>H56-68. To znamená, že obojsmerný „útok“ (G23=68) a (AD7=68) vedie k tomu, že iba čísla 6 a 8 môžu byť v I8 a I9 Ďalej (I89=68) je spojené s „. útok“ na H56 spolu s predchádzajúcimi podmienkami, čo vedie k H56-68. Okrem tohto "útoku" je pripojený (ABC4=689), ktorý v v tomto príklade vyzerá nadbytočne, ale ak by sme pracovali bez pracovného listu, potom by bol impakt faktor (ABC4=689) skrytý a bolo by vhodné mu venovať osobitnú pozornosť.

Ďalšia akcia: I5=2>G1-2,G6-9,B6-4,B5-2.

Dúfam, že je to už jasné bez komentárov: nahraďte čísla, ktoré sú za pomlčkou, nebudete sa mýliť:

H7=9>I7-4; D6=8>D1-4,H6-6>H5-8:

Nasledujúca séria akcií:

D3=2; D8=1>A9-1>A2-2>A3-4,G9-3;

(D8=1)+(G9=3)>G8-7>G7-1>G5-5;

D5=9>E5-6>F5-4:

I=4>C9-4>C7-2>E9-2>EF7-35>B7-7,F89-89,

to znamená, že v dôsledku „prečiarknutia“ – odstránenia nadbytočných číslic – sa v bunkách F8 a F9 objaví otvorený „nahý“ pár 89, ktorý sa spolu s ostatnými výsledkami uvedenými v položke použije na tabuľku:

H2=4>H3-1>F2-1>F1-6>A1-3>B8-3,C8-5,H1-7>I2-5>I3-3>I4-7>H4-3

Ich výsledok:

Potom vykonajte pomerne bežné, zrejmé akcie:

H1=7>C1-8>E1-5>F3-7>E2-9>E3-8,C3-9>B3-5>B2-6>C2-7>C4-6>A4-9>B4- 8;

B2=6>B9-9>A8-6>I8-8>F8-9>F9-8>I9-6;

E7=3>F7-5,E6-7>F6-3

Ich výsledok: konečné riešenie problému:

Tak či onak budeme predpokladať, že „základné“ metódy v sudoku alebo iných oblastiach intelektuálneho využitia sme na základe vhodného modelu na to prišli a dokonca sa naučili ich používať. Ale to je len časť nášho pokroku v metodológii riešenia problémov. Ďalej, opakujem, nasleduje nie vždy zohľadňovaná, ale nevyhnutná fáza privádzania predtým naučených metód do stavu jednoduchého používania. Riešenie príkladov, pochopenie výsledkov a metód tohto riešenia, prehodnotenie tohto materiálu na základe prijatého modelu, opätovné premyslenie všetkých možností, dotiahnutie stupňa ich pochopenia k automatizácii, keď sa riešenie pomocou „základných“ ustanovení stáva rutinou a zaniká ako problém. Čo to dáva: toto by mal zažiť každý. Ide však o to, že keď sa problémová situácia stane rutinou, vyhľadávací mechanizmus intelektu smeruje k zvládnutiu čoraz zložitejších ustanovení v oblasti riešených problémov.

Čo sú „zložitejšie ustanovenia“? Sú to len nové „základné“ ustanovenia pri riešení problému, ktorého pochopenie sa dá zas priviesť do stavu jednoduchosti, ak sa nájde vhodný model na tento účel.

V článku Vasilenko S.L. "Number Harmony Sudoku" Našiel som príklad problému s 18 symetrickými klávesmi:

V súvislosti s týmto problémom sa tvrdí, že sa dá vyriešiť pomocou „základných“ techník len do určitého stavu, po ktorom už zostáva len použiť jednoduché vyhľadávanie so skúšobnou náhradou niektorých domnelých exkluzívnych (jednotných, jednoduchých) číslic do bunky. Tento stav (pokročilý o niečo ďalej ako vo Vasilenkovom príklade) má tvar:

Existuje taký model. Toto je druh rotačného mechanizmu pre identifikované a neidentifikované výhradné (jednotné) čísla. V najjednoduchšom prípade sa určitá trojica exkluzívnych číslic otáča doprava alebo doľava a presúva túto skupinu z riadku do riadku alebo zo stĺpca do stĺpca. Vo všeobecnosti sa tri skupiny trojíc čísel otáčajú jedným smerom. Vo viac ťažké prípady, tri páry exkluzívnych čísel rotujú v jednom smere a tri páry singlov rotujú v opačnom smere. Takže napríklad exkluzívne číslice v prvých troch riadkoch uvažovaného problému sú otočené. A čo je najdôležitejšie, tento druh rotácie si môžete všimnúť pri pohľade na usporiadanie čísel v spracovanom pracovnom hárku. Tieto informácie sú zatiaľ dostatočné a v procese riešenia problému pochopíme ďalšie nuansy rotačného modelu.

Takže v prvých (horných) troch riadkoch (1, 2 a 3) si môžeme všimnúť rotáciu párov (3+8) a (7+9), ako aj (2+x1) s neznámym x1 a trojka dvojhry (x2+4+ 1) s neznámou x2. Pritom môžeme zistiť, že každé z x1 a x2 môže byť 5 alebo 6.

Riadky 4, 5 a 6 sa pozerajú na dvojice (2+4) a (1+3). Chýbať by mala aj tretia neznáma dvojica a trojka singlov, z ktorých je známy len jeden počet, 5.

Podobne sa pozrieme na riadky 789, potom na trojice stĺpcov ABC, DEF a GHI. Zozbierané informácie zapíšeme symbolickou a dúfam, že celkom zrozumiteľnou formou:

Nateraz potrebujeme len tieto informácie na pochopenie všeobecnej situácie. Dobre si to premyslite a potom môžeme prejsť k nasledujúcej tabuľke špeciálne pripravenej na tento účel:

Alternatívne možnosti som zvýraznil farbami. Modrá znamená „povolené“ a žltá „zakázaná“. Ak je povedzme povolené A2=79 v A2=7, potom C2=7 je zakázané. Alebo naopak – A2=9 je povolené, C2=9 je zakázané. A potom sa povolenia a zákazy prenášajú v logickom reťazci. Toto sfarbenie je vytvorené tak, aby uľahčilo zobrazenie rôznych alternatívnych možností. Vo všeobecnosti je to určitá analógia k vyššie uvedeným metódam „x-wing“ a „swordfish“ pri spracovaní tabuliek.

Pri pohľade na možnosť B6=7 a teda B7=9 môžeme okamžite zistiť dva body, ktoré nie sú kompatibilné s touto možnosťou. Ak B7=9, potom sa v riadkoch 789 objaví synchrónne rotujúca trojica, čo je neprijateľné, pretože buď len tri páry (a s nimi asynchrónne tri singly) alebo tri trojky (bez singlov) sa môžu otáčať synchrónne (v jednom smere). Okrem toho, ak B7=9, potom po niekoľkých krokoch spracovania listu v 7. riadku zistíme nekompatibilitu: B7=D7=9. Takže nahradíme jedinú prijateľnú z dvoch alternatívnych možností B6 = 9 a potom sa problém vyrieši pomocou jednoduchých prostriedkov konvenčného spracovania bez akéhokoľvek slepého vyhľadávania:

Ďalej mám hotový príklad pomocou rotačného modelu na vyriešenie problému z majstrovstiev sveta v sudoku, ale tento príklad vynechávam, aby tento článok nebol príliš dlhý. Okrem toho, ako sa ukázalo, tento problém má tri možné riešenia, čo nie je vhodné pre počiatočný vývoj modelu rotácie číslic. Strávil som tiež dosť času premýšľaním nad problémom Garyho McGuira, stiahnutým z internetu, so 17 kľúčmi na vyriešenie jeho hádanky, kým som s ešte väčším podráždením zistil, že táto „skladačka“ má viac ako 9 tisíc možných riešení. .

Takže, chtiac-nechtiac, musíme prejsť k „najzložitejšiemu“ problému sudoku na svete, ktorý vyvinul Arto Incala a ktorý, ako vieme, má jedinečné riešenie.

Po zadaní dvoch veľmi zjavných exkluzívnych čísel a spracovaní hárka problém vyzerá takto:

Klávesy priradené k pôvodnej úlohe sú zvýraznené čiernym a väčším písmom. Aby sme v riešení tohto problému postúpili, musíme sa opäť spoľahnúť na adekvátny model vhodný na tento účel. Tento model je akýmsi mechanizmom na otáčanie čísel. V tomto a predchádzajúcich článkoch sa o tom už diskutovalo viackrát, ale aby sme pochopili ďalší materiál článku, mal by sa tento mechanizmus premyslieť a podrobne rozpracovať. Asi tak, ako keby ste s takýmto mechanizmom pracovali desať rokov. Ale stále budete schopní pochopiť tento materiál, ak nie z prvého čítania, potom z druhého alebo tretieho atď. Navyše, ak preukážete vytrvalosť, privediete tento „ťažko pochopiteľný“ materiál do stavu jeho rutiny a jednoduchosti. V tomto ohľade nie je nič nové: to, čo je spočiatku veľmi ťažké, sa postupne stáva menej ťažkým a s ďalším nepretržitým rozvádzaním všetko, čo je najzreteľnejšie a nevyžaduje si duševnú námahu, zapadne na svoje správne miesto, po ktorom sa môžete uvoľniť. mentálny potenciál pre ďalší pokrok v danom riešenom probléme alebo ohľadom iných problémov.

Pri dôkladnej analýze štruktúry problému Arto Incal si možno všimnúť, že je celý postavený na princípe troch synchrónne rotujúcich párov a troch singlov rotujúcich asynchrónne na páry: (x1+x2)+(x3+x4)+(x5 +x6)+(x7+x8+ x9). Poradie otáčania môže byť napríklad nasledovné: v prvých troch riadkoch 123 prvý pár (x1+x2) prechádza z prvého riadku prvého bloku do druhého riadku druhého bloku, potom do tretieho riadku. tretieho bloku. Druhý pár preskočí z druhého radu prvého bloku do tretieho radu druhého bloku, potom v tomto otočení preskočí na prvý riadok tretieho bloku. Tretí pár z tretieho riadku prvého bloku skočí do prvého riadku druhého bloku a potom v rovnakom smere otáčania prejde do druhého riadku tretieho bloku. Trojka singlov sa pohybuje v podobnom režime rotácie, ale v opačnom smere ako rotácia dvojíc. Situácia so stĺpcami vyzerá podobne: ak je tabuľka mentálne (alebo skutočne) otočená o 90 stupňov, potom sa riadky stanú stĺpcami s rovnakým vzorom pohybu singlov a párov ako predtým pre riadky.

Vykonaním týchto rotácií v našej mysli v súvislosti s problémom Arto Incala postupne pochopíme zjavné obmedzenia výberu možností pre túto rotáciu pre vybranú trojicu riadkov alebo stĺpcov:

Nemali by existovať synchrónne (v rovnakom smere) rotujúce trojice a páry - takéto trojčatá, na rozdiel od trojčiat singlov, sa v budúcnosti budú nazývať trojčatami;

Nemali by existovať žiadne asynchrónne páry alebo asynchrónne singly;

Nemali by sa tam otáčať dvojice ani jednotlivci rovnakým (napríklad správnym) smerom – ide o opakovanie predchádzajúcich obmedzení, ale možno sa to bude zdať zrozumiteľnejšie.

Okrem toho existujú ďalšie obmedzenia:

V 9 riadkoch by nemal byť jediný pár, ktorý sa zhoduje s párom v žiadnom zo stĺpcov, a to isté platí pre stĺpce a riadky. Malo by to byť zrejmé: pretože samotná skutočnosť, že dve čísla sú umiestnené na rovnakom riadku, naznačuje, že sú v rôznych stĺpcoch.

Môžeme tiež povedať, že veľmi zriedka sa vyskytujú zhody dvojíc v rôznych trojiciach riadkov alebo podobná koincidencia v trojiciach stĺpcov a tiež zriedkavo zhody trojíc singlov v riadkoch a/alebo stĺpcoch, ale tieto sú takpovediac pravdepodobnostné. vzory.

Štúdia blokov 4,5,6.

V blokoch je možných 4-6 párov (3+7) a (3+9). Ak prijmeme (3+9), dostaneme neprijateľnú synchrónnu rotáciu trojky (3+7+9), takže máme pár (7+3). Po nahradení tohto páru a následnom spracovaní tabuľky konvenčnými prostriedkami získame:

Zároveň môžeme povedať, že 5 v B6=5 môže byť iba singletónové, asynchrónne (7+3) a 6 v I5=6 je parageneratívne, pretože sa nachádza v rovnakom riadku H5=5 v šiestom bloku, a preto nemôže byť sama a môže sa pohybovať iba synchrónne s (7+3.

a zoradil kandidátov na nezadaných podľa toho, koľkokrát sa objavili v tejto úlohe v tejto tabuľke:

Ak pripustíme, že najčastejšie 2, 4 a 5 sú jednotlivci, tak podľa pravidiel striedania s nimi možno kombinovať iba dvojice: (7+3), (9+6) a (1+8) - pár (1 +9) zahodený, pretože neguje dvojicu (9+6). Ďalej po nahradení týchto párov a singlov a ďalšom spracovaní tabuľky pomocou obvyklých metód získame:

Takto sa tabuľka ukázala ako neposlušná: nechce sa spracovať až do konca.

Budete sa musieť namáhať a všimnúť si, že v stĺpcoch ABC je pár (7+4) a že 6 sa v týchto stĺpcoch pohybuje synchrónne so 7, teda 6 je paragenerátor, takže v stĺpci „C“ 4. bloku iba sú možné kombinácie (6+3) +8 alebo (6+8)+3. Prvá z týchto kombinácií nefunguje, odvtedy sa v 7. bloku v stĺpci „B“ objaví neplatná synchrónna trojica - trojica (6+3+8). Nuž a potom po dosadení možnosti (6+8)+3 a spracovaní tabuľky bežným spôsobom dospejeme k úspešnému dokončeniu úlohy.

Druhá možnosť: vráťme sa k tabuľke získanej po identifikácii kombinácie (7+3)+5 v riadkoch 456 a prejdeme k skúmaniu stĺpcov ABC.

Tu si môžeme všimnúť, že dvojica (2+9) sa nemôže vyskytovať v ABC. Iné kombinácie (2+4), (2+7), (9+4) a (9+7) dávajú synchrónny triplet v A4+A5+A6 a B1+B2+B3, čo je neprijateľné. Zostáva jeden prijateľný pár (7+4). Okrem toho sa 6 a 5 pohybujú synchrónne 7, čo znamená, že sú paragenerujúce, t.j. vytvorte pár párov, ale nie 5+6.

Urobme si zoznam možných párov a ich kombinácií so singlami:

Kombinácia (6+3)+8 nefunguje, pretože v opačnom prípade sa v jednom stĺpci (6+3+8) vytvorí neplatná trojica, o ktorej už bola reč a ktorú si overíme ešte raz zaškrtnutím všetkých možností. Z kandidátov na dvojhru boduje najviac číslo 3 a zo všetkých uvedených kombinácií je najpravdepodobnejšia: (6+8)+3, t.j. (C4=6 + C5=8) + C6=3, čo dáva:

Ďalej, najpravdepodobnejší kandidát na sólo je 2 alebo 9 (každý 6 bodov), avšak v každom z týchto prípadov zostáva platný kandidát 1 (4 body). Začnime s (5+29)+1, kde 1 je asynchrónne s 5, t.j. Dajme 1 z B5=1 ako asynchrónny singleton do všetkých stĺpcov ABC:

V bloku 7, stĺpec A, sú jediné možné možnosti (5+9)+3 a (5+2)+3. Mali by sme však venovať pozornosť tomu, že v riadkoch 1-3 sa teraz objavujú dvojice (4+5) a (8+9). Ich nahradenie vedie k rýchlemu výsledku, t.j. dokončiť úlohu po spracovaní tabuľky bežnými prostriedkami.

Teraz, keď sme si precvičili predchádzajúce možnosti, môžeme sa pokúsiť vyriešiť problém Arto Incal bez použitia štatistických odhadov.

Opäť sa vrátime do východiskovej polohy:

V blokoch je možných 4-6 párov (3+7) a (3+9). Ak prijmeme (3+9), dostaneme neprijateľnú synchrónnu rotáciu trojky (3+7+9), takže pre dosadenie do tabuľky máme len možnosť (7+3):

5 tu, ako vidíme, je single, 6 je paraforming. Platné možnosti v ABC5: (2+1)+8, (2+1)+9, (8+1)+9, (8+1)+2, (9+1)+8, (9+1) +2. Ale (2+1) je asynchrónne (7+3), takže zostáva (8+1)+9, (8+1)+2, (9+1)+8, (9+1)+2. V každom prípade je 1 synchrónna (7+3), a teda paragenerujúca. Dosadíme do tabuľky 1 v tejto funkcii:

Číslo 6 je tu paragenerátor v bloku. 4-6, ale nápadný pár (6+4) nie je v zozname platných párov. Preto štyri v A4 = 4 sú asynchrónne 6:

Keďže D4+E4=(8+1) a podľa rotačnej analýzy tvorí túto dvojicu, dostaneme:

Ak bunky C456=(6+3)+8, potom B789=683, t.j. dostaneme synchrónny triplet, takže nám zostane možnosť (6+8)+3 a výsledok jej substitúcie:

B2=3 je tu jediný, C1=5 (asynchrónny 3) je paragenerujúci, A2=8 je tiež paragenerujúci. B3=7 môže byť synchrónne aj asynchrónne. Teraz sa môžeme dokázať v zložitejších technikách. Cvičeným okom (alebo aspoň pri kontrole na počítači) vidíme, že pre akýkoľvek stav B3=7 – synchrónny alebo asynchrónny – dostaneme rovnaký výsledok A1=1. Túto hodnotu teda môžeme dosadiť do A1 a potom obyčajnejšími jednoduchými prostriedkami splniť našu, respektíve Arto Incalovu úlohu:

Tak či onak sme boli schopní zvážiť a dokonca ilustrovať tri všeobecné prístupy k riešeniu problémov: určiť bod pochopenia problému (nie predpokladaný alebo slepo deklarovaný, ale skutočný moment, od ktorého môžeme hovoriť o pochopení problém), zvoliť si model, ktorý nám umožní realizovať porozumenie prostredníctvom prirodzeného alebo myšlienkového experimentu a – to je tretia vec – priviesť mieru pochopenia a vnímania dosiahnutých výsledkov do stavu samozrejmosti a jednoduchosti. Existuje aj štvrtý prístup, ktorý osobne používam.

Každý človek zažíva stavy, keď sa intelektuálne úlohy a problémy, ktorým čelí, riešia ľahšie, ako je to bežné. Tieto podmienky môžu byť úplne reprodukované. Aby ste to dosiahli, musíte ovládať techniku ​​​​vypínania myšlienok. Najprv aspoň na zlomok sekundy, potom sa tento moment vypnutia stále viac naťahuje. V tomto ohľade nemôžem hovoriť ďalej, alebo skôr odporučiť, pretože dĺžka používania tejto metódy je čisto osobná záležitosť. Ale k tejto metóde sa niekedy uchýlim z dlhej chvíle, keď stojím pred problémom, že nevidím možnosti, ako sa k nemu postaviť a vyriešiť ho. Výsledkom je, že skôr či neskôr sa zo zásobníc pamäti vynorí vhodný prototyp modelu, ktorý objasní podstatu toho, čo je potrebné vyriešiť.

Incalov problém som vyriešil niekoľkými spôsobmi, vrátane tých, ktoré sú popísané v predchádzajúcich článkoch. A vždy som v tej či onej miere používal tento štvrtý prístup s vypnutím a následným sústredením mentálneho úsilia. Najrýchlejšie riešenie problému som získal jednoduchým hľadaním - to, čo sa nazýva "metóda poke" - avšak s použitím iba "dlhých" možností: tých, ktoré by mohli rýchlo viesť k pozitívnemu alebo negatívnemu výsledku. Ďalšie možnosti mi zabrali viac času, pretože väčšinu času zabral aspoň hrubý vývoj technológie na využitie týchto možností.

Dobrá možnosť je aj v duchu štvrtého prístupu: nalaďte sa na riešenie problémov sudoku, pričom v procese riešenia problému dosaďte do bunky iba jedno číslo. To znamená, že väčšina úlohy a jej údajov sa „posúva“ v mysli. Takto prebieha väčšina intelektuálneho procesu riešenia problémov a je to zručnosť, ktorú by ste mali trénovať, aby ste zvýšili svoje schopnosti riešiť problémy. Napríklad nie som profesionálny riešiteľ sudoku. Mám iné úlohy. Chcem si však stanoviť nasledujúci cieľ: získať schopnosť riešiť problémy sudoku so zvýšenou zložitosťou, bez pracovného hárka a bez toho, aby som sa uchýlil k nahradeniu viac ako jedného čísla do jednej prázdnej bunky. V tomto prípade je povolený akýkoľvek spôsob riešenia sudoku, vrátane jednoduchého vymenovania možností.

Nie náhodou si spomínam na zoznam možností. Akýkoľvek prístup k riešeniu problémov sudoku zahŕňa vo svojom arzenáli súbor určitých metód, vrátane jedného alebo druhého typu vyhľadávania. Navyše, ktorákoľvek z metód používaných najmä v Sudoku alebo pri riešení akýchkoľvek iných problémov má svoju vlastnú oblasť efektívnej aplikácie. Takže pri rozhodovaní o jednoduché úlohy Sudoku je najúčinnejšie s jednoduchými „základnými“ metódami, opísanými v mnohých článkoch na túto tému na internete, a zložitejšia „metóda rotácie“ je tu často zbytočná, pretože len komplikuje pohyb. jednoduché riešenie a zároveň niektoré nové informácie, ktorá sa prejavuje v priebehu riešenia problému, neposkytuje. Ale v najťažších prípadoch, ako je problém Arta Incala, môže hrať kľúčovú úlohu „metóda rotácie“.

Sudoku v mojich článkoch je len názorným príkladom prístupov k riešeniu problémov. Medzi problémami, ktoré som riešil, sú aj také, ktoré sú rádovo ťažšie ako sudoku. Napríklad počítačové modely kotlov a turbín umiestnené na našej webovej stránke. Tiež by mi nevadilo o nich hovoriť. Ale zatiaľ som si vybral sudoku, aby som svojim mladým spoluobčanom dostatočne jasne ukázal možné cesty a etapy napredovania ku konečnému cieľu riešených problémov.

To je na dnes všetko.

História hry

Číselná štruktúra bola vynájdená vo Švajčiarsku už v 18. storočí, na jej základe bola v 20. storočí vyvinutá číselná krížovka. V USA, kde bola samotná hra vynájdená, sa však nerozšírila, na rozdiel od Japonska, kde sa hlavolam nielen udomácnil, ale získal si aj veľkú obľubu. V Japonsku získalo známy názov „Sudoku“ a potom sa rozšírilo do celého sveta.

Pravidlá hry

Krížovka má jednoduchú štruktúru: je určená matica 9 políčok, nazývaných sektory. Tieto štvorce sú usporiadané tri v rade a majú veľkosť 3x3 bunky. Matica sudoku vyzerá ako štvorec pozostávajúci z 3 riadkov a 3 stĺpcov, ktoré ju rozdeľujú na 9 sektorov, z ktorých každý obsahuje 9 buniek. Niektoré bunky sú vyplnené číslami – čím viac čísel poznáte, tým je hádanka jednoduchšia.

Účel hry

Musíte vyplniť všetky prázdne bunky a existuje len jedno pravidlo: čísla by sa nemali opakovať. Každý sektor, riadok a stĺpec musí obsahovať čísla od 1 do 9 bez opakovania. Prázdne bunky je lepšie vyplniť ceruzkou: uľahčí to vykonávanie zmien v prípade chyby alebo začiatok odznova.

Metódy riešenia

Pozrime sa na jednoduchú verziu Sudoku. Napríklad v sektore alebo riadku zostáva iba 1 prázdna bunka - je logické, že do nej musíte zadať číslo, ktoré nie je v číselnom rade.

Ďalej stojí za to preskúmať riadky a stĺpce, ktoré majú rovnaké čísla v 2 sektoroch. Keďže čísla by sa nemali opakovať, môžete skontrolovať, v ktorých bunkách sa rovnaké číslo môže nachádzať v 3. sektore. Často zostáva len 1 bunka, do ktorej stačí zadať číslo.

Tým sa vyplní časť poľa krížovky. Potom môžete začať študovať struny. Povedzme, že v riadku sú 3 voľné bunky, chápete, aké čísla tam treba zadať, ale neviete, kde presne. Treba vyskúšať náhradu. Často existujú možnosti, keď číslo nemožno nájsť v ostatných 2 bunkách, pretože je buď v príslušnom stĺpci alebo v sektore.

Náročné sudoku

V komplexnom sudoku fungujú tieto metódy len na polovicu, prichádza čas, keď je úplne nemožné určiť, do ktorej bunky zadať číslo. Potom musíte urobiť predpoklad a otestovať ho. Ak sú v riadku, stĺpci alebo sektore 2 bunky, do ktorých je rovnako možné zadať číslo, musíte ho zadať ceruzkou a ďalej postupovať podľa logiky vyplnenia. Ak je váš predpoklad nesprávny, v určitom bode krížovka ukáže chybu a čísla sa budú opakovať. Potom je zrejmé, že číslo by malo byť v druhej bunke, musíte sa vrátiť a opraviť chybu. V tomto prípade je lepšie použiť farebnú ceruzku, aby ste ľahšie našli bod, v ktorom musíte krížovku opäť vyriešiť.

Malé tajomstvo

Riešenie Sudoku je jednoduchšie a rýchlejšie, ak si najprv ceruzkou označíte, aké čísla môžu byť v každej bunke. Potom nebudete musieť zakaždým kontrolovať všetky sektory a počas procesu vypĺňania budú okamžite zrejmé tie bunky, v ktorých zostane iba 1 variant platného čísla.

Sudoku nie je len vzrušujúca hra, ktorá vám umožní tráviť čas, je to hádanka, ktorá sa vyvíja logické myslenie, schopnosť uchovávať veľké množstvo informácií a zmysel pre detail.

V tomto článku sa podrobne pozrieme na to, ako vyriešiť zložité sudoku pomocou príkladu diagonálneho sudoku.

Dostaneme podmienku číslo 437, ktorá je znázornená na obrázku 1. A hneď vám padne do oka prvý štvorec, ktorý je najviac nasýtený otvorenými číslami. Chýbajú čísla 1, 3, 4, 9. Ale keďže vodorovná čiara a už obsahuje tri, číslo tri je umiestnené na c1. Zvyšok nemôžeme presne umiestniť. Poďme sa teda pozrieť na to, čo ešte máme. Napríklad vertikála je 4 a tu môže byť číslo štyri iba na b4, kvôli prítomnosti štvorky v piatom poli a na horizontálnom c. Zvyšné čísla zatiaľ neuvádzame.

Všetky techniky a metódy, ktoré budeme ďalej používať, sa vzťahujú na riešenie jednoduchého aj zložitého sudoku.

Čo máme na vodorovnom b? Troch je tu málo a môže stáť len na b8. (V druhom štvorci už je tam a na kolmici 9). A ak budeme ďalej pozorne skúmať vodorovnú čiaru b, zistíme, že máme skrytý singel – číslo 9 na bunke b9. Pretože ostatní kandidáti (to sú 1 a 5) nemôžu stáť na tejto bunke!

Čo môžeme urobiť ďalej? Ak vezmeme do úvahy štvorec päť. Tu môžu byť čísla 3 a 5 buď na d5 alebo e6. To znamená, že tieto bunky neuvažujeme pre zvyšné čísla Na základe toho zostáva jediné miesto na jednotku - bunka d6.

Výsledok našich akcií je znázornený na obrázku 2. Vďaka našej analýze je riadok b úplne vyplnený. Jeden na b5, päť na b6. Čo nám dáva právo umiestniť 3 a 5 v piatom poli!

Pokračujme v analýze piateho štvorca. Chýba mu číslica 7, nie je na hlavných uhlopriečkach a čo je najzaujímavejšie na kolmici 4. Práve vďaka tejto kolmici môžeme s istotou povedať, že sedmička v piatom políčku môže byť buď na f4 resp. e4. Keďže vodorovné čiary c a d už obsahujú sedem. A nemôže stáť na e5 kvôli vertikále 4. Ďalej sa obráťme na hlavné horizontály. A potom sú hneď umiestnené sedmičky! Na i9 a f4.

Čo sme dostali, je možné vidieť na obrázku 3. Ďalej budeme pokračovať v analýze hlavných uhlopriečok. Ak sa pozrieme na ten vychádzajúci zo štvorca a1, tak mu chýba dvojka, ktorá je umiestnená len na h8. Aj tejto uhlopriečke chýbajú 1, 8 a 9. 1 možno umiestniť len na a1, dajte to rýchlo! Ale osmička nemôže stáť na d4, keďže je už na vodorovnej d. Usporiadame - d4 -9, e5 -8.

Teraz však môžeme úplne vyplniť piate a prvé políčko! To, čo sme dostali, je znázornené na obrázku 4.

Dávajte pozor na vertikálu 3. Tu musíte umiestniť 1, 6, 7. Jednotka je umiestnená iba na f3 a na základe toho sú umiestnené ostatné - e3 -7, h3-6. Ďalšou v poradí máme vertikálu 9, keďže jej umiestnenie je jednoducho famózne. d9-2, g9-6, h9-8.

Čo ak skontrolujeme otvorené dvojhry?! Napríklad číslo tri je bezpečne umiestnené na bunkách d2 a h5. Aj keď ďalšia analýza singletonov nič neprináša. Potom sa obrátime na zostávajúcu uhlopriečku. Chýba jej 6, 2, 4. Číslo šesť môže byť len na c7. Zvyšok je ľahké vyplniť.

Prečo nie je vertikálna 4 nastavená na koniec? Poďme to napraviť. s4-8.

Výsledok nášho výskumu je znázornený na obrázku 5. Teraz vyplníme vodorovnú čiaru c. s8-1, s5-9, s6-2. A to všetko je založené na prítomnosti týchto čísel v iných vertikálach. Na základe horizontálneho c je ľahké vyplniť horizontálne d. d1-6, d7-4. Potom je tretí štvorec celkom jednoducho vyplnený. Ale druhé námestie ešte nie je zaplnené, hoci kandidáti sú tiež len dvaja – šiesti a siedmi. Ale nevyskytujú sa pozdĺž vertikál päť a šesť, a preto ich zatiaľ dáme bokom.

Po analýze všetkých vertikál a horizontál sme dospeli k záveru, že nie je možné jednoznačne uviesť jedno číslo. Preto prejdime k zvažovaniu štvorcov. Obráťme sa na šiesty štvorec. Chýba tu 5,6,8,9. Ale určite môžeme umiestniť čísla 6 a 8 na bunky f7 a f8. Vďaka našej analýze je vyznačená celá vodorovná čiara f! f1 -9, f2 -5. A tu vidíme, že štvrtý štvorec je úplne zaplnený! e1-4, e2-2.

To, čo sme dostali, je možné vidieť na obrázku 6. Teraz sa obráťme na štvorec deväť. Máme tu jeden otvorený singel – číslo jeden na i7. Vďaka čomu môžeme dať jednotku do siedmeho štvorca na g2. Osem na i2.